• 資料請求のお申込み
  • 学習カウンセリングのお申込み
  • 無料体験授業のお申込み

メニュー
「春の学習計画を整えて、新学年で差をつける」
プロの学習カウンセリングはこちら
モチアカ式 中学受験お悩みズバッと！診断
中学受験に役立つ受験情報を配信するSS-1公式LINEはこちら
SS-1の無料資料ダウンロード
13歳から身につけたい やる気アップ勉強法
モチアカ式 中学受験お悩みズバッと！診断
中学受験に役立つ受験情報を配信するSS-1公式LINEはこちら
SS-1の無料資料ダウンロード
13歳から身につけたい やる気アップ勉強法

【中学受験】「時計算」の裏ワザ!? 苦手な時計算が簡単に解けるテクニック（第1回）

最終更新
カテゴリー：算数の勉強法
算数の中学受験対策は
中学受験個別指導のSS-1
【中学受験】「時計算」の裏ワザ!? 苦手な時計算が簡単に解けるテクニック（第1回）

第1回「小さい方の角度を求める」
第2回「『重なる・反対方向・直角』の時間」
第3回「『比』を使って解く時計算の極意」

中学受験の算数において、多くの受験生が苦手意識を持ちやすい「時計算」。
実は、ルールさえマスターしてしまえば、パズルを解くようにスラスラと答えを出すことができるのです。そのやり方を身につけていきましょう。

今回は、基本となる「小さい方の角度を求める」テクニックを、わかりやすく整理して解説します。

  1. 時計算を攻略する「3つの裏技」
  2. 実践！例題を解いてみよう「小さい方の角度を求める」
  3. 「わかったつもり」で終わらせないために

時計算を攻略する「3つの裏技」

時計算を解く前に、まずは以下の3点を頭に叩き込みましょう。

これだけで、「時計算」が驚くほどシンプルに見えてきます。

1. 「長針」と「短針」の「速さ」を覚える

時計算とはそもそも、「速さ」という大きな単元の中にある一つの小さな単元です。
「旅人算」なら「人」、流水算なら「船」が動くように、時計算では「針」が動きます。

時計には長針と短針があり、これらが進むのは「長さ」ではなく「角度」です。
まずは、それぞれの「動く速さ」を確認しましょう。

  1. 長針の速さ：分速6°（長針は60分で時計を1周します。つまり、60分で360°回転するので、1分あたり「360° ÷ 60分 ＝ 6°」進みます）
  2. 短針の速さ：分速0.5°（短針は12時間で時計を1周（360°）します。1時間（60分）では30°進むため、1分あたり「30° ÷ 60分 ＝ 0.5°」進みます）

2. 「旅人算」として言いかえて解く

次に、時計算を簡単に解くための裏ワザは、「時計算＝旅人算（追いかけ算）」考えて、言いかえて解くことです。

たとえば、今回の「小さい方の角」であれば

時計の文字盤を「丸い池」に見立ててみましょう。「長針さん」が、前を歩く「短針さん」を後ろから追いかけているイメージです。普通の旅人算との違いは、縮めていくものが「きょり」ではなく「角度」になっていることだけです。

2つの針は同時に動いて追いかけっこをします。ここで重要になるのが、「1分間にどれだけ角度の差が縮まるのか（あるいは広がるのか）」ということです。これも計算して覚えてしまいましょう。

1分間に縮まる（広がる）角度：分速5.5° （長針の分速6° － 短針の分速0.5° ＝ 5.5°）

3. スタート位置は必ず「〇時ちょうど」にする

裏ワザの3つ目は、「スタート地点を決める」ということです。

「兄は家から学校に向かって～」とスタートする場所が決まっている通常の旅人算と違って、時計算には明確なスタート地点が書かれていません。ゆえに、「『◯時ちょうど』をスタート地点にする」と自分の中でルール化してしまいましょう。

例）6時20分のとき、長針と短針が作る小さい方の角度は何度ですか。
→スタート地点を「6時ちょうど（6時00分）」に設定し、そこから旅人算（追いかけ算）を使って求めます。

この3つの裏技を身につければ、時計算は簡単に解けるようになります。さっそく下の問題で練習してみましょう！

実践！例題を解いてみよう「小さい方の角度を求める」

では、実際に問題を解いてテクニックの使い方を確認しましょう。

問題①

5時12分のとき、長針と短針が作る小さい方の角度は何度ですか。

解き方のステップ

① スタート地点（5時ちょうど）の角度を出す

まずは「5時00分」のときの二人の間のきょり（へだたり）を調べます。

時計の文字盤は、1メモリが30°なので、

30° × 5メモリ = 150°・・・スタート時、二人は 150° 離れているとわかります。

② 5時12分のときの角度を求める

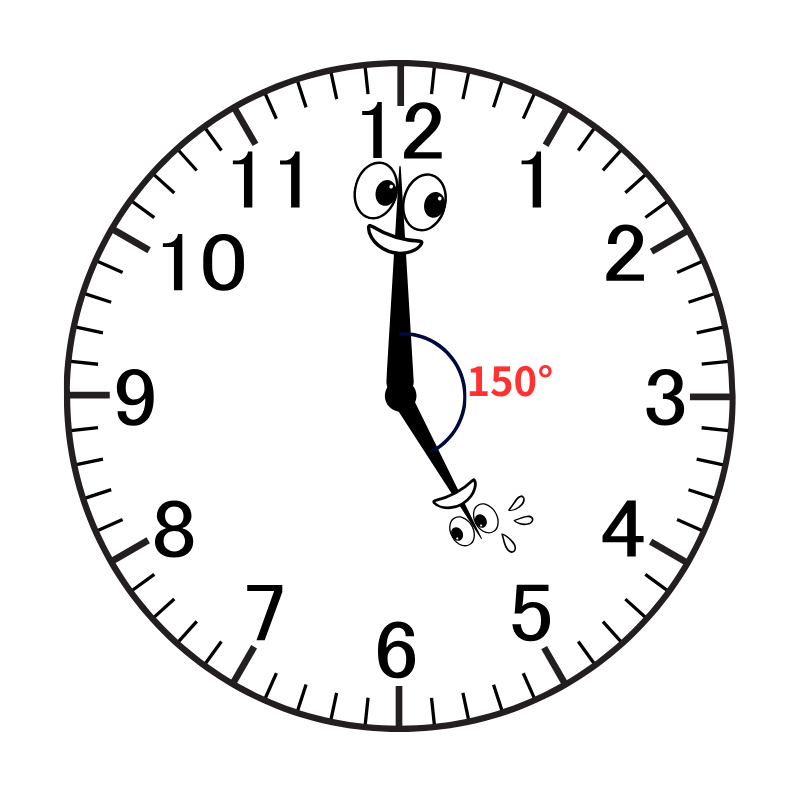
「5時12分のとき、長針と短針が作る小さい方の角度は何度」を言いかえると、「5時12分のとき、二人の間の角度（きょり）は何度」となります。このように言いかえることでイメージがつきやすいのではないでしょうか。

①で、スタート地点で二人は150°離れていました。そこから、1分間に 5.5° ずつ差が縮まっていくので、5時12分では、合計「5.5° × 12分 = 66°」の差が縮まることになります。

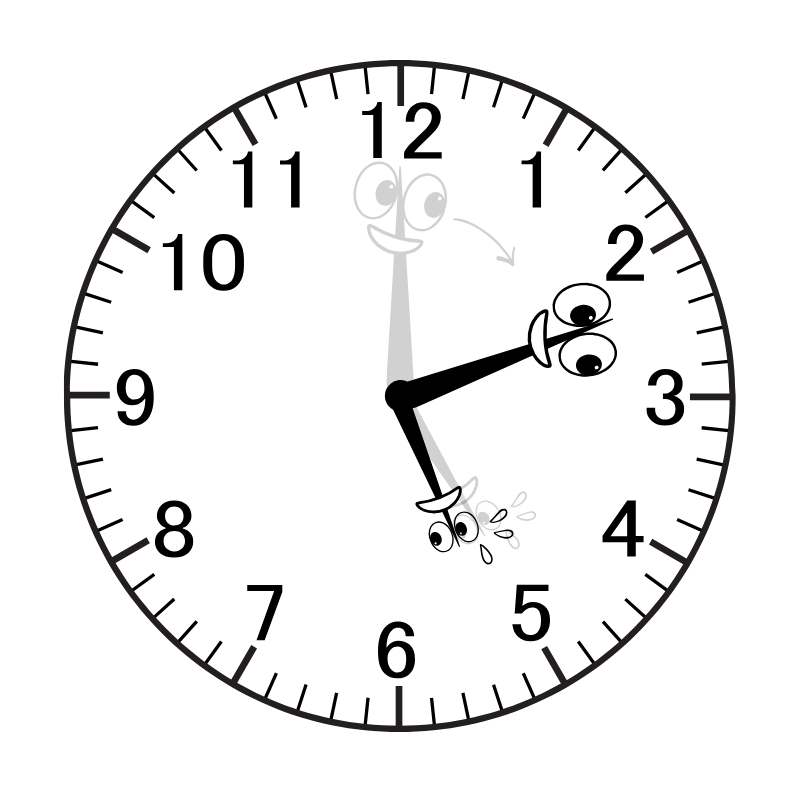
よって、5時12分の小さい方の角度は「150° - 66° = 84°」となります。

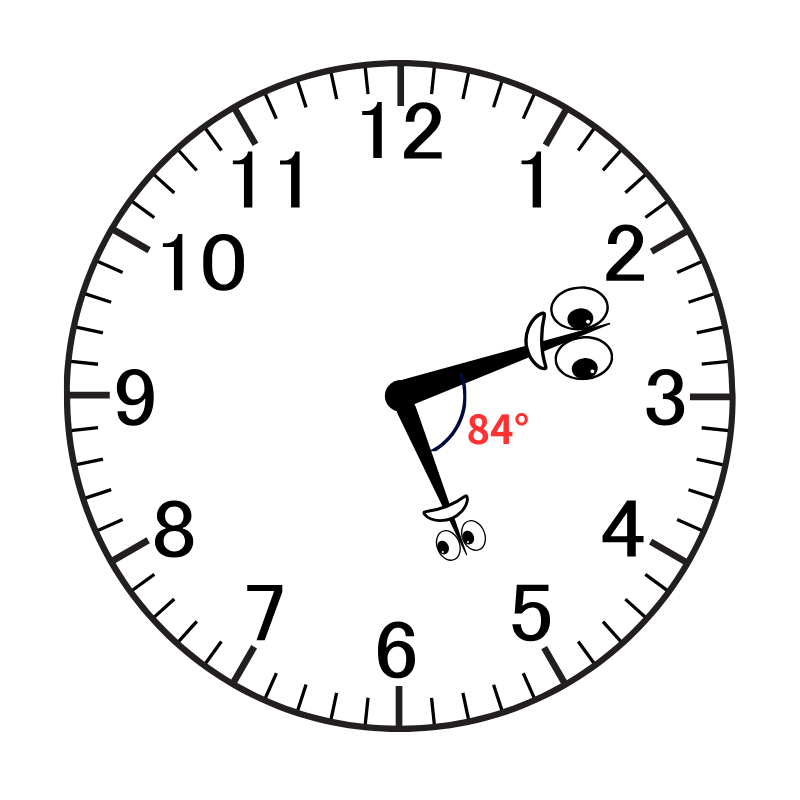
答え）84°

問題②

11時38分のとき、長針と短針が作る小さい方の角度は何度ですか。

解き方のステップ

① スタート地点（11時ちょうど）の角度を出す

まずは「11時00分」のときの二人の間のきょり（へだたり）を調べます。

時計の文字盤は、数字1つ分（1メモリ）が 30°です。

30° × 11メモリ = 330°・・・スタート時、二人は 330° 離れている

〈注意！〉
「長針さん」も「短針さん」も「時計回り」に動きます。
「長針さん」が反時計回りに進まないよう注意しましょう。

② 38分間で「縮まった角度」を出す

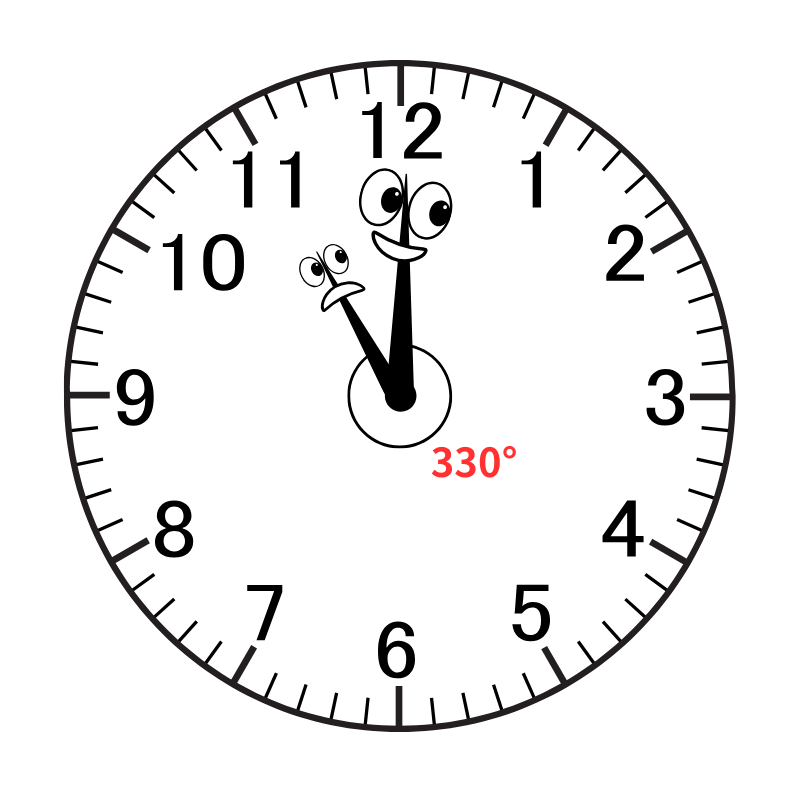
1分間に 5.5° ずつ差が縮まっていくので、

11時38分では、合計「5.5° × 38分 = 209°」の差が縮まることになります。

はじめの二人の差が「330°」でしたから、

11時38分の小さい方の角度は「330° - 209° = 121°」となります。

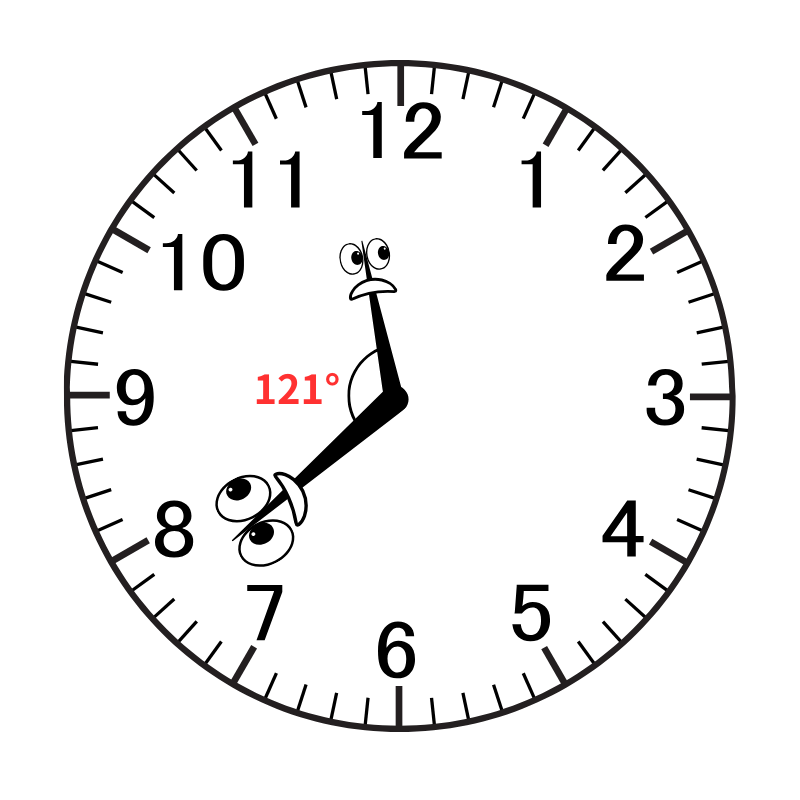
答え）121°

問題③

8時7分のとき、長針と短針が作る小さい方の角度は何度ですか。

解き方のステップ

① スタート地点（8時ちょうど）の角度を出す

まずは「8時00分」のときの二人の間のきょり（へだたり）を調べます。

時計の文字盤は、数字1つ分（1メモリ）が 30°です。

30° × 8メモリ = 240°・・・スタート時、二人は 240° 離れている

② 7分間で「縮まった角度」を出す

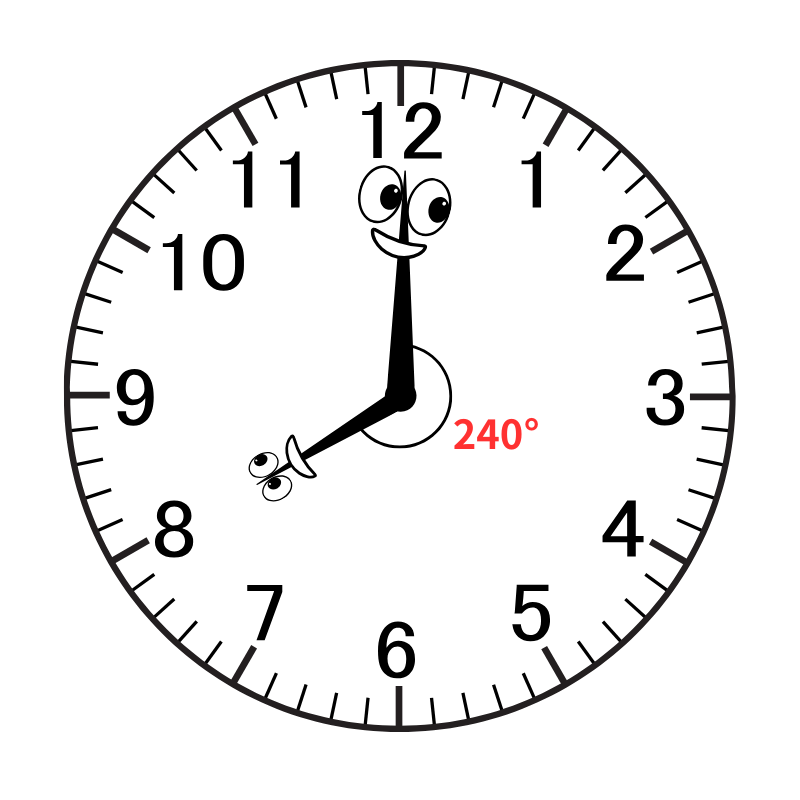
1分間に 5.5° ずつ差が縮まっていくので、

8時7分では、合計「5.5° × 7分 = 38.5°」の差が縮まることになります。

はじめの二人の差が「240°」でしたから、

8時7分のときの角度は「240° - 38.5° = 201.5°」となります。

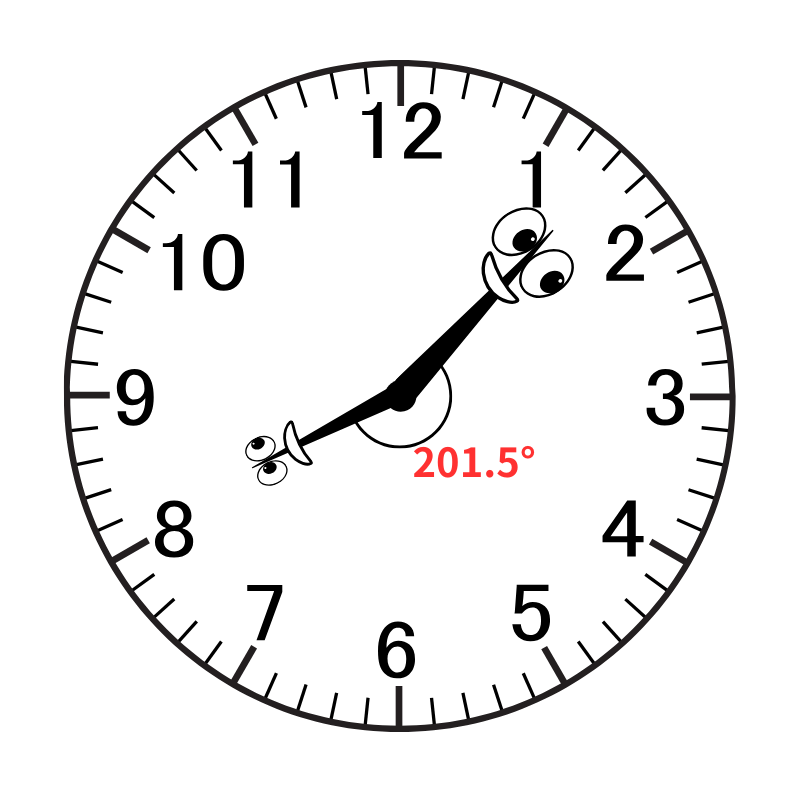
〈注意！〉
ここで次のことに気をつけましょう。

【答えが180°よりも大きいときは、360°が引く】

今回は201.5°だったので、180°よりも大きいです。
つまり、小さい方の角ではありませんね。

この場合は、360°から引いて答えを求めます。

360° - 201.5° = 158.5°

答え）158.5°

「わかったつもり」で終わらせないために

時計算の基本、「小さい方の角度を求めるテクニック」はいかがでしたか？ 「なんだ、意外と簡単じゃないか！」と感じた方も多いかもしれません。

しかし、中学受験の算数はここからが本番です。 基本のルールを理解したあと、「お子さん一人で、初見の問題に対応できるか」は全く別の話になります。

  • 「家で教えるとわかるのに、テストになると間違える」
  • 「式の意味を答えられない（丸暗記してしまっている）」
  • 「途中計算のミスが減らない」

もし、このようなお悩みをお持ちであれば、それは単なる「練習不足」ではなく、「学習のやり方」そのものに原因があるかもしれません。

SS-1の学習カウンセリングでは、プロの講師がマンツーマンでお子さんの答案用紙やノートを分析し、「なぜ点数が伸び悩んでいるのか」「今、何をすべきなのか」を明確にします。

「時計算」だけでなく、お子さんの算数の成績を最短でアップさせるための「次の一手」を、一緒に見つけませんか？

まずは無料の学習カウンセリングで、お気軽にご相談ください。

tabata.png

この相談に答えた講師
田畠 靖大(Tabata Yasuhiro)
中学受験専門のプロ個別指導教室SS-1(エスエスワン)関東副代表・渋谷教室長。関東にあるSS-1渋谷教室を中心に多くの受験生を指導し、毎年難関中学に送り出しています。担当教科は国語・算数。論理性を重視しながらも、ソフトな語り口でお子様の課題解決に取り組みます。テストでの得点向上のみならず、科目の根本理解、体系理解を実現、得意科目に仕上げていきます。

算数の中学受験対策は
中学受験個別指導のSS-1

関連記事

新着記事

中学受験に役立つ受験情報を配信するSS-1公式LINEはこちら
中学受験情報をお届けするSS-1の無料メルマガ

SS-1の無料メルマガ『Challenge Eyes』では、中学受験専門の個別指導ノウハウが詰まった塾の成績アップ情報をお届けしています。

オンライン対応